Resumen
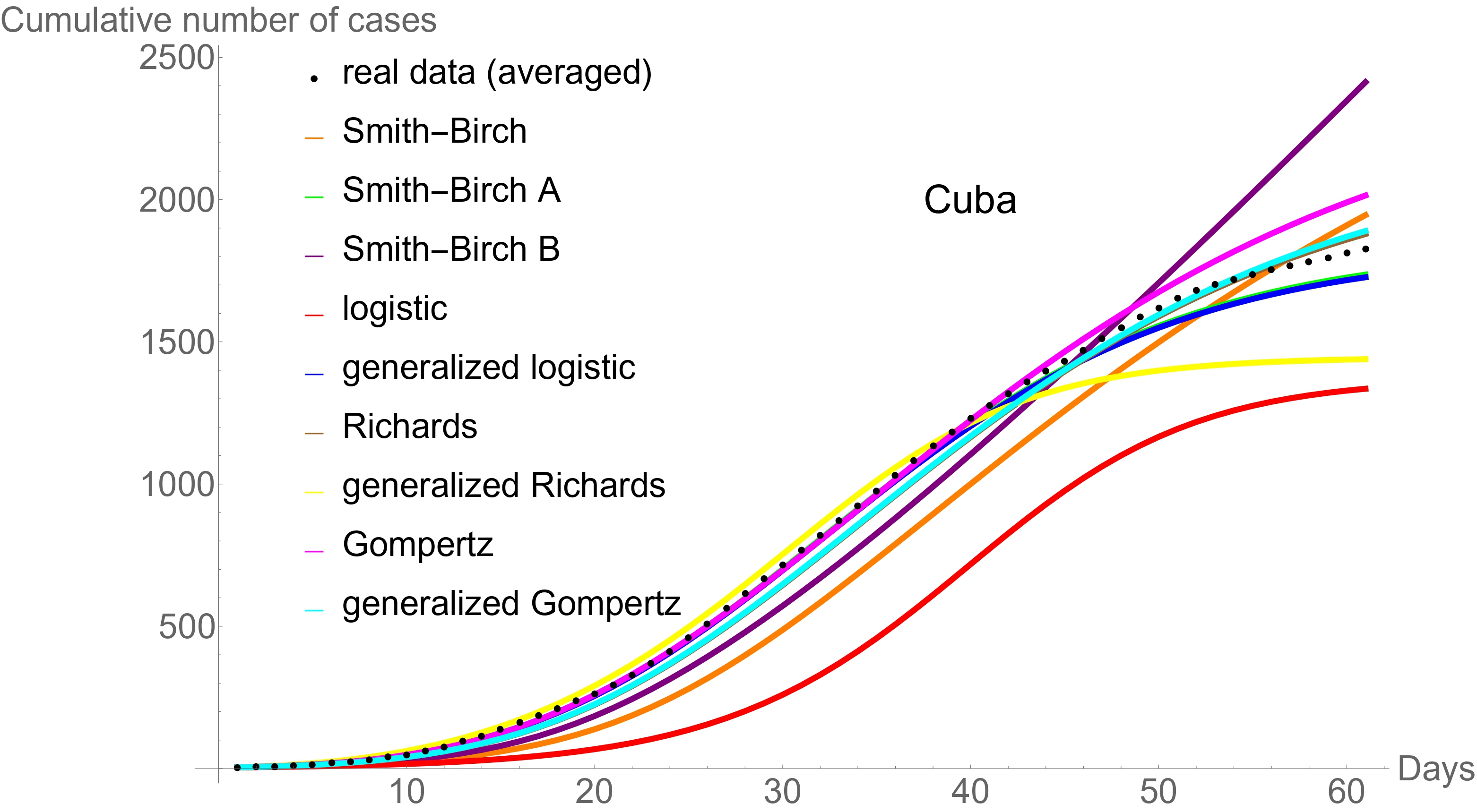
Las curvas en forma de S o curvas sigmoidales pueden definirse como soluciones de ecuaciones diferenciales autónomas de primer orden que cumplen con cuatro condiciones, a través de las cuales se demuestra sin necesidad de resolverlos que los modelos de la familia logística generalizada y el de Smith-Birch tienen soluciones sigmoidales. Se introducen dos generalizaciones del modelo de Smith-Birch, cuyas soluciones son curvas sigmoidales para cierto rango de variación de los parámetros. Se encontraron series temporales del número cumulativo de casos para los 61 primeros días de la pandemia de COVID-19 en algunos países donde los nuevos modelos aquí introducidos predicen mejor la propagación de la enfermedad que los modelos tradicionales de la familia logística.
Referencias
[1] V. Vieira, Comput. Ecol. Soft. 10, 162 (2020).
[2] F. H. Eeckman and W. J. Freeman, Brain Res. 557, 13 (1991).
[3] K. Sandberg, B. M. Bibby, B. Timmermans, A. Cleeremans, and M. Overgaard, Conscious. Cogn. 20, 1659 (2011).
[4] D. R. F. Paul E. Smaldino, Lucy M. Aplin, Sci. Rep. 8, 14015 (2018).
[5] J. M. J. Murre, Psychon. Bull. Rev. 21, 344 (2014).
[6] C. L. T. D. Tab Rasmussen, J. Hum. Evol. 23, 159 (1992).
[7] H. Qiu, K. Durand, H. Rabinovitch-Chable, M. Rigaud, V. Gazaille, P. Clavère, and F. G. Sturtz, Biotechniques 42, 355 (2007).
[8] S. Pixton and R. Howe, J. Stored. Prod. Res. 19, 1 (1983).
[9] A. G. A. Anna M. Michałowska-Kaczmarczyk and Tadeusz Michałowski, J. Anal. Sci., Methods and Instrumentation 4, 27 (2014).
[10] C. Y. Hsieh, S. L. Fang, Y. F. Wu, Y. C. Chu, and B. J. Kuo, Hortic. 7, 537 (2021).
[11] S. H. Austin, T. R. Robinson, W. D. Robinson, and R. E. Ricklefs, Methods Ecol. Evol. 2, 43 (2011).
[12] M. Michalczu, K. Damaziak, and A. Goryl, Ann. Anim. Sci. 16, 65 (2016).
[13] L. Cao, P.-J. Shi, L. Li, and G. Chen, Symmetry 11, 204 (2019).
[14] T. Onoda, R. Yamamoto, K. Sawamura, Y. Inoue, A. Matsui, T. Miyake, and N. Hirai, J. Equine Sci. 22, 37 (2011).
[15] Y. Zhang, A. Biswas, and V. I. Adamchuk, Geoderma 289, 1 (2017).
[16] K. Hufkens, R. Ceulemans, and P. Scheunders, Ecol. Inform. 3, 97 (2008).
[17] B. G. Akre and D. M. Johnson, J. Anim. Ecol. 48, 703 (1979).
[18] J. I. Lehr Brisbin and M. C. Newman, Water Air Soil Poll 57-58, 691 (1991).
[19] L. A. Kuznar and W. G. Frederick, Ecol. Econ. 46, 296 (2003).
[20] I. McGowan, The Statistician 35, 73 (1985).
[21] K. Kobayashi, W. A. Borders, S. Kanai, K. Hayakawa, H. Ohno, and S. Fukami, Appl. Phys. Lett. 119, 132406 (2021).
[22] D. S. Paolino and M. P. Cavatorta, Fatigue Fract. Eng. Mater. Struct. 36, 316 (2012).
[23] M. El-Khawaga, S. El-Badawy, and A. Gabr, Arabian J. Sci. Eng. 45, 3973 (2020).
[24] S. Mastilovíc, Theor. Appl. Mech. 45, 95 (2018).
[25] D. Jang, G. Chae, and S. Shin, Sens. 15, 25385 (2015).
[26] B. Lu, H. He, H. Yu, H.Wang, G. Li, M. Shi, and Dongpu, Sens. 20, 7197 (2020).
[27] D. Kucharavy and R. D. Guio, Procedia Eng. 9, 559 (2011).
[28] R. Bürger, G. Chowell, and L. Y. Lara-D´ıaz, Math. Biosci. 334 (2021), ISSN 18793134.
[29] F. Brauer, C. Castillo-Chavez, and Z. Feng, Mathematical Models in Epidemiology, Texts in Applied Mathematics (Springer, New York, NY, 2019).
[30] G. Zhou and G. Yan, Emerg. Infect. Dis. 9 (2003), ISSN 10806040.
[31] B. Pell, Y. Kuang, C. Viboud, and G. Chowell, Epidemics 22 (2018), ISSN 18780067.
[32] D. W. Shanafelt, G. Jones, M. Lima, C. Perrings, and G. Chowell, EcoHealth 15 (2018), ISSN 16129210.
[33] L. Dinh, G. Chowell, K. Mizumoto, and H. Nishiura, Theor. Biology Med. Model. 13 (2016), ISSN 17424682.
[34] S. Zhao, S. S. Musa, H. Fu, D. He, and J. Qin, Parasit. Vectors. 12 (2019), ISSN 17563305.
[35] B. Malavika, S. Marimuthu, M. Joy, A. Nadaraj, E. S. Asirvatham, and L. Jeyaseelan, Clin. Epidemiol. Glob. Health. 9 (2021), ISSN 22133984.
[36] C. Y. Shen, IJID 96 (2020), ISSN 18783511.
[37] K. Wu, D. Darcet, Q. Wang, and D. Sornette, medRxiv (2020).
[38] G. L. Vasconcelos, A. M. Macdo, R. Ospina, F. A. Almeida, G. C. Duarte-Filho, A. A. Brum, and I. C. Souza, Peer J 2020 (2020), ISSN 21678359.
[39] K. Roosa, Y. Lee, R. Luo, A. Kirpich, R. Rothenberg, J. M. Hyman, P. Yan, and G. Chowell, J. Clin. Med. 9 (2020), ISSN 20770383.
[40] K. Roosa, Y. Lee, R. Luo, A. Kirpich, R. Rothenberg, J. M. Hyman, P. Yan, and G. Chowell, Infect. Dis. Model. 5 (2020), ISSN 24680427.
[41] Y. Wu, L. Zhang, W. Cao, X. Liu, and X. Feng, Front. Phys. 8, 566 (2021), ISSN 2296-424X.
[42] M. López, A. Peinado, and A. Ortiz, PLoS ONE 16
(2021), ISSN 19326203.
[43] P. Pincheira-Brown and A. Bentancor, Epidemics 37 (2021), ISSN 18780067.
[44] M. T. Pérez-Maldonado, J. Bravo-Castillero, R. Mansilla, and R. O. Caballero-P´erez, Nova scientia 14, 18 (2022).
[45] G. Jarne, J. Sanchez-Choliz, and F. Fatas-Villafranca, Evol. Inst. Econ. Rev. 3, 239 (2007).
[46] L. S. Pontriaguin, Ecuaciones Diferenciales Ordinarias (Editorial Pueblo y Educación, La Habana, 1981).
[47] M. Carrillo and J. M. González, Technol. Forecasting Social Change 69, 233 (2002).
[48] W. G. Bardsley and R. E. Childs, Biochem. J. 149, 313 (1975).
[49] Z. Li, B. S. Yang Zhang, Z. Xing, and Q. Wang, Electronics 11, 1365 (2022).
[50] R. Gomeni and C. Gomeni, Comput. Biomed. Res. 13, 489 (1980).
[51] H. Li, X. Jiang, G. Huo, C. Su, B. Wang, Y. Hu, and Z. Zheng, nt. J. Adv. Manuf. Technol. 119, 1531 (2022).
[52] P. Verhulst, Corr. Math. Physics 10, 113 (1838).
[53] A. Tsoularis and J. Wallace, Math. Biosci. 179 (2002), ISSN 00255564.
[54] M. H. Zwietering, I. Jongenburger, F. M. Rombouts, and K. van’t Riet, Appl. Environ. Microbiol. 56, 1875 (1990).
[55] J. Schnute, Can. J. Fish. Aquat. Sci. 38, 1128 (1981).
[56] K. M. C. T. Erve and E. T. Erve, Ecol. Modell. 359, 117 (2017).
[57] F. E. Smith, Ecol. 44, 651 (1963).
[58] C. P. D. Birch, Ann. Bot. 83, 713 (1999).
[59] M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (Dover, New York, 1964), ninth dover printing, tenth gpo printing edition.
[60] R. M. May, Nature 261, 459 (1976), ISSN 20522541.
[61] W. E. Boyce and R. C. DiPrima, Elementary Differential Equations (John Wiley & Sons, Inc., Hoboken, NJ, 2012).
[62] A. L.-M. J. A. Mesejo-Chiong, Ciencias Matemáticas 34, 19 (2020).

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial 4.0.
Derechos de autor 2025 Sociedad Cubana de Física & Facultad de Física de la Universidad de La Habana